いかに計算するか

それでは計算方法を考えていきたいと思います。いろいろ数字を置いていかないと定量的な議論ができないので、理屈っぽい話が続きます。

まず、1日の勤務時間を10時～17時（弊社はまさにこの時間帯）と置いて、昼休みを除くとすると1日でランダムに「トイレに行く」と選択できる時間は、午前２時間・午後４時間の合計6時間と考えることができます。

この6時間のうちに「私はランダムに6回トイレに行く」と考えても良いのですが、そうすると「午前中に6回トイレに行って午後は行かない」という極端な場合も含んでしまいますし、実はこちらのほうが計算が複雑になるので、いくつかの時間帯に区切って、その中で「トイレに1回行く」という考え方で進めます。
ここは切り良く1時間＝60分に1回トイレに行くことを考え、その時間帯（60分）でトイレに行くタイミングはランダムとします。つまり、60分単位のうち最初のほうにトイレに行くか、最後のほうに行くかは私の気分次第ということです。

私（男）のトイレに費やす時間は用を足すことはもちろん、通路を通ることや手を洗うことを含めることと、数字を切り良くするために5分としました。結果として「気分でトイレに行くこと」は12個（60分÷5分）のタイミングをランダムに選んでいることと同義になります。
逆に言えば区切った1時間を迎えると、1回分のトイレのタイミングを、最初に12面あるサイコロを振って決めているようなものです。「トイレ」という言葉を連呼して不思議な気持ちになっていましたが、なんとなく算数の問題っぽくなってきました。

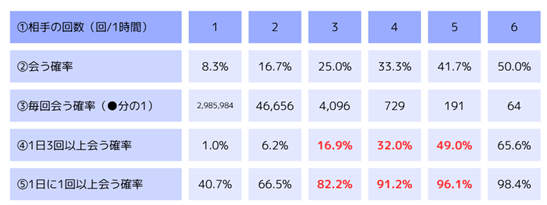
ここまでくると、まず一つ単純な答えを得ることができます。相手が私と同様に「1日6回」の頻度であるならば各時間帯でタイミングは12通りあるため、「12面のサイコロを振って彼と私で同じ数字が出る確率」と「トイレで偶然出会う確率」は同じになります。その確率を計算すると全144パターン（12×12）のうち、12パターン存在するので、約8%（12分の1）です。10回に1回よりも少ないです。

さらに毎回会う、つまり連続して起こるとなると、1日でタイミングが6回あるので、「毎回（6回）トイレで会う」確率は300万分の1と計算できます。（約8％の6乗）
「10分の1に満たない確率」が6回連続で続くと考えていただけると、どれぐらいレアな事象なのかイメージが付くかと思います。
ちなみに「1日に”1回は会う”確率」ですら約40％と、2日に1回会う程度の確率となりました。
他の人に当てはめてみると、確かにこれくらいのペースが感覚として合っているように思えます。1日に「1回以上会う確率（40.7％）」よりも「1度も会わない確率（59.3％）」のほうが大きいわけですから、毎日会わないことのほうが確率としては自然です。少なくとも毎日”彼”には会っているので、やはり「ペースが同じだけど偶然会っている（理由①）」は説明がつかないように思えます。

それでは具体的に、相手の回数がどれくらい増えると、「毎回会う」ようになるのでしょうか。私のトイレに行く頻度が「1時間1回」であることは変わらず、単純に相手の回数が増えるとどうなるか考えていきたいと思います。計算自体は、私のサイコロの面の数は12面で変わらず、相手のサイコロの面の数が少なくなった場合を計算するので簡単です。
単純に相手の頻度が2倍、3倍になればなるほど出会う数が増え、相手が1時間に6回 トイレに行く＝1時間の半分（30分）をトイレで過ごすようになると、当たり前ですが遭遇する確率が50：50になります。しかし、2倍、3倍と確率が上がったとしても、私が毎回（1日6回）彼と出会う確率は微々たるものでした。具体的には「相手が1時間に6回トイレに行く＝1時間に会う確率が50％」だとしても、1日のトイレに行く6回中6回出会う確率は64分の1と、2％にも満たない確率だと算出されました。

ふと、考えてみると確かに毎回（1日6回）遭遇しているかというとそういう訳ではないので、毎日3回、4回遭遇すると「毎回会っている」と思い込んでいるのではないかと考えました。他の人は数日に1回会う程度ですから。

そうすると、同じ頻度（私も相手も1日6回トイレに行く）の前提で、1日3回以上（3回～6回）出会う確率は1％となりました。毎回（6回）会う確率が300万分の1でしたので、3回～5回会う場合を含めただけでも現実的な数字になりました。それでも1％と非常に稀な確率ですが。
ここから、さらに相手の頻度が2倍（1日12回）、3倍（1日18回）になると遭遇する確率が6.2％、16.9％となることが分かりました。先ほどの確率と違って、頻度が2倍、3倍になっても単純に確率も2倍、3倍にならないところがおもしろいです。

なお、詳しい方のために補記しておくと、確率の算出にあたっては、N=6の2項分布を想定して計算しています。

算出した確率を見てみると、出会う確率が50％（相手が1日の半分はトイレにいることになる）でも、1日3回以上会う確率が65.6％ですから、なかなか毎日に遭遇するというのは意外と難しいものですね。
私の「毎日毎回トイレで会う」という主観を「週のうち数日、その日は少なくとも3回以上会う」ということに再定義すると、相手のトイレの回数が「1時間に3回～5回の確率」が現実的な確率（16.9％～49.0％）になりました。

さすがに1時間に5回（＝1時間のうち25分はトイレに費やす）は社会人としてあり得ないかと思うので、問題にならない範囲として妥当なのは3回（＝1時間のうち15分はトイレに費やす）でしょうか。

結論としては、私の3倍の頻度でトイレに行っているということになりました。

ちなみに「1日1回は出会う確率」も算出すると相手が1時間に3回トイレに行く場合は82％、4回行く場合は91％ということになります。少なくとも1日1回は会っている自信があるので3～4倍という検証結果は正しそうです。（私と同じ頻度の人は確率が41％と2～3日に1回会う程度と肌感覚に合っている一方で、やっぱり1日に数回会うということは少し異常ですね。）

絶滅危惧種の数え方と同じ

なお、今回相手のトイレの回数を推定した考え方は特別に編み出したものではなく、絶滅危惧種の個体総数を推定する手法を応用したものです。

生物の個体数や絶滅危惧種の個体群など、観察が困難な集団の総数を推定するために用いられる統計的方法です。（捕獲再捕獲法または標識再捕獲法と呼ぶそうです。）さすがに「すべての個体を捕まえて数え上げる」という力技は時間も労力も途方もなくかかるため、簡単な統計知識を使って個体数を推定しています。

具体的には第1回捕獲（初回調査）で、調査対象となる生物を捕獲し、電子タグ等の標識をつけた後に放します。例えば、100匹の鯨を捕まえ、そのすべてに標識をつけて海に戻すとします。再捕獲（第2回調査）として、一定期間後、再びランダムに個体を捕まえます。そうすると標識が付いた個体と付いていない個体が混ざっているので、標識のついた個体の割合を算出します。たとえば、50匹の鯨を再捕獲し、そのうち10匹に標識が付いていたものとします。

そうすると、第1回調査で標識を付けた個体数と第2調査で測定した標識が付いていた割合から個体総数が想定でき、前述の例では個体総数が500匹（100÷20%）と推定できます。

この調査も第1回調査で標識を付けた個体を、第2回調査で偶然全て捕まえてしまうという可能性もあるため、何回も続けることによって偶然の要素を排除し、正確な生態系の調査へ繋げていきます。ちなみに、アクチュアリーになるための試験問題でも、過去に同様の問題が出されたことがあります。

このように、アクチュアリーである私は偶然の出来事を一般の人がドン引きするくらい定量的に見ています。一般的な言語情報として「稀に」や「よくある」とか「少ない」といった抽象的な情報をとことん数字に落として考えると、見ている事象（今回でいうと相手のトイレの頻度）はもちろん、自分の主観も具体的な数字に落とされることが面白いです。また、数字に落とすことによって例えば宝くじに当たる確率、不謹慎ですが交通事故に巻き込まれる確率とも横比較ができるので、確率というものを「よくあること」なのか「稀（レア）なことなのか」具体的に捉えることができます。

さて今回の検証では「相手は1時間のうち、トイレタイムで15分～20分は費やしている」ということが言えるので、やはり相手は結構仕事をさぼっているな、ということが分かりました。加えて、前述のとおり上下関係の些細な恨みもあって「毎回トイレに居やがって。」と散々文句を垂れてしまいましたが、毎日かつ毎回でないことが分かり、私も反省する必要があることが分かりました。

アクチュアリーという人種は、このように車を運転していて信号につかまったときや電車の乗り換えがうまくいかなかったとき等の日常の出来事を、それは偶然だった（運が悪かったのか）のか必然だったのか（よくあることなのか）、常に気にしてしまいながら日々を過ごしています。